LAWS AND RULES OF BOOLEAN ALGEBRA

LAWS AND RULES OF BOOLEAN ALGEBRA

Laws of Boolean Algebra

The basic laws of Boolean algebra-the commutative laws for addition and multiplication, the associative laws for addition and multiplication, and the distributive law-are the same as in ordinary algebra:

1.     Commutative law

2.     Associative law

3.     Distributive law

4.     Identity law

5.     Zero and one law

6.     Inverse law

7.     De Morgan’s law

8.     Idempotent law

9.     Absorption law

10.   Double Complement Law

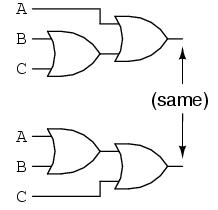
Commutative laws

The commutative law of addition for two variables is written as

A+B = B+A

This law states that the order in which the variables are ORed makes no difference. Remember, in Boolean algebra as applied to logic circuits, addition and the OR operation are the same. Illustrates the commutative law as applied to the OR gate and shows that it doesn't matter to which input each variable is applied.

For addition

A + B = B + A

The commutative law of multiplication for two variables is

A.B = B.A

This law states that the order in which the variables are ANDed makes no difference.

For multiplication

A B = B A

Associative laws

The associative law of addition is written as follows for three variables:

A + (B + C) = (A + B) + C

This law states that when ORing more than two variables, the result is the same regardless of the grouping of the variables. Illustrates this law as applied to 2-input OR gates.

For addition

A + (B + C) = (A + B) + C

The Associative law of multiplication is written as follows for three

variables:

A(BC) = (AB)C

This law states that it makes no difference in what order the variables are grouped when ANDing more than two variables. Illustrates this law as applied to 2-input AND gates.

For multiplication

A(BC) = (AB)

Distributive law

The distributive law is written for three variables as follows:

A(B + C) = AB + AC

This law states that ORing two or more variables and then ANDing the result with a single variable is equivalent to ANDing the single variable with each of the two or more variables and then ORing the products. The distributive law also expresses the process of factoring in which the common variable A is factored out of the product terms, for example,

AB + AC = A(B + C).Illustrates the distributive law in terms of gate implementation.

A(B + C) = AB + AC

Boolean expressions can be simplified or manipulated. Table shows basic laws of Boolean Algebra to help manipulating logic equations.

	AND Form	OR Form
Identity Law	A.A=A	A+0=A
Zero and One Law	A.0=A	A+1=1
Inverse Law	A.A̅=0	A+A̅=1
Idempotent Law	A.A=A	A+A=A
Commutative Law	A.B=B.A	A+B=B+A
Associative Law	A.(B.C)=(A.B).C	A+(B+C)=(A+B)+C
Distributive Law	A+(B.C)=(A+B).(A+C)	A.(B+C)=(A.B)+(A.C)
Absorption Law	A(A+B)=A	A+A.B=A A+A’B=A+B
DeMorgan’s Law	(A.B)=A̅+B̅	(A̅+̅B̅)=A̅.B̅
Double Complement Law	X̿=X	X̿=X

Rules of Boolean Algebra

Below are 12 basic rules that are useful in manipulating and simplifying Boolean expressions. Rules 1 through 9 will be viewed in terms of their application to logic gates. Rules 10 through 12 will be derived in terms of the simpler rules and the laws previously discussed.

1.  A + 0 = A                     7. A . A = A

2.  A + 1= 1                      8. A . A̅ = 0

3.  A . 0 = 0                       9.  A̅̅ = A

4.  A . 1 = A                       10. A + AB = A

5.  A + A = A                     11. A + A̅B = A + B

6.  A + A̅ = 1                     12. (A + B)(A + C) = A + BC

Rule 1                        A + 0 = A

A variable ORed with 0 is always equal to the variable. If the input variable A is 1, the output variable X is 1, which is equal to A. If A is 0, the output is 0, which is also equal to A.The lower input is fixed at 0.

Rule 2                        A + 1 = 1

A variable ORed with 1 is always equal to 1. A 1 on an input to an OR gate produces a 1 on the output, regardless of the value of the variable

on the other input. Where the lower input is fixed at 1.

Rule 3                        A . 0 = 0

A variable ANDed with 0 is always equal to 0. Any time one input to an

AND gate is 0, the output is 0, regardless of the value of the variable on the other input. where the lower input is fixed at 0.

Rule 4           A . 1 = A

A variable ANDed with 1 is always equal to the variable. If A is 0 the output of the AND gate is 0. If A is 1, the output of the AND gate is 1 because both inputs are now 1s. where the lower input is fixed at 1.

Rule 5           A + A = A

A variable ORed with itself is always equal to the variable. If A is 0, then 0 + 0 = 0; and if A is 1, then 1 + 1 = 1. where both inputs are the same variable.

Rule 6                        A + A̅ = 1

A variable ORed with its complement is always equal to 1. If A is 0, then 0 + 0 = 0 + 1 = 1. If A is l, then 1 + 1 = 1+ 0 = 1. where one input is the complement of the other.

Rule 7                        A . A = A

A variable ANDed with itself is always equal to the variable. If A = 0,

then 0.0 = 0; and if A = 1. then 1.1 = 1.

Rule 8           A . A = 0

A variable ANDed with its complement is always equal to 0. Either A or A will always be 0: and when a 0 is applied to the input of an AND gate. The output will be 0 also.

Rule 9           A = A̿

The double complement of a variable is always equal to the variable. If you start with the variable A and complement (invert) it once, you get A̅. If you then take A̅ and complement (invert) it, you get A, which is the original variable.

Rule 10        A + AB = A

This rule can be proved by applying the distributive law, rule 2, and rule 4 as follows:

A + AB = A( 1 + B)                        Factoring (distributive law)

= A . l                                                 Rule 2: (1 + B) = 1

= A                                         Rule 4: A . 1 = A

Shows the truth table and the resulting logic circuit simplification.

Rule 11        A + A̅B = A + B

This rule can be proved as follows:

A + A̅B = (A + AB) + A̅B              Rule 10: A = A + AB

= (AA + AB) + A̅B                         Rule 7: A = AA

=AA +AB +AA̅ +A̅B                      Rule 8: adding AA̅ = 0

= (A + A̅)(A + B) Factoring

= 1. (A + B)                                      Rule 6: A + A̅ = 1

=A + B                                   Rule 4: drop the 1

Shows the truth table and the resulting logic circuit simplification.

Rule 12        (A + B)(A + C) = A + BC

This rule can be proved as follows:

(A + B)(A + C) = AA + AC + AB + BC              Distributive law

= A + AC + AB + BC                                  Rule 7: AA = A

= A( 1 + C) + AB + BC                             Rule 2: 1 + C = 1

= A. 1 + AB + BC                                       Factoring (distributive law)

= A(1 + B) + BC                                          Rule 2: 1 + B = 1

= A. 1 + BC                                                  Rule 4: A . 1 = A

= A + BC

shows the truth table and the resulting logic circuit simplification.

De MORGAN’S THEOREMS

De Morgan, a mathematician who knew Boole, proposed two theorems that are an important part of Boolean algebra.In practical terms. De Morgan's theorems provide mathematical verification of the equivalency of the NAND and negative-OR gates and the equivalency of the NOR and negative-AND gates.

De Morgan’s theorem is stated as follows:

The complement of a product of variables is equal to the sum of the complement of the variables.

The formula for expressing this theorem for two variables is:

                                      X̅Y̅  =  X̅  +  Y̅

De Morgan’s theorem is stated as follows:

The complement of a sum of variables is equal to the product of the complements of the variables

The formula for expressing this theorem for two variables is:

                             X+Y  =  X̅  *  Y̅

shows the gate equivalencies and truth tables for the two equations above.

STANDARD FORMS OF BOOLEAN EXPRESSIONS

All Boolean expressions, regardless of their form, can be converted into

either of two standard forms: the sum-of-products form or the product-of sums form. Standardization makes the evaluation, simplification, and

implementation of Boolean expressions much more systematic and easier.

The Sum-of-Products (SOP) Form

When two or more product terms are summed by Boolean addition,

the resulting expression is a sum-of-products (SOP). Some examples are:

AB + ABC

ABC + C̅DE + B̅CD̅

AB + BCD + AC

Also, an SOP expression can contain a single-variable term, as in

A + ABC̅ + BCD̅.

In an SOP expression a single overbar cannot extend over more than

one variable.

The Standard SOP Form

So far, you have seen SOP expressions in which some of the product

terms do not contain all of the variables in the domain of the expression. For example, the expression A̅BC̅ + AB̅D + ABC̅D̅ has a domain made up of the variables A, B, C. and D. However, notice that the complete set of variables in the domain is not represented in the first two terms of the expression; that is, D or D̅ is missing from the first term and C or C̅ is missing from the second term. A standard SOP expression is one in which all the variables in the domain appear in each product term in the expression. For example, A̅BCD̅ + ABC̅D + AB̅CD is a standard SOP expression.

Converting Product Terms to Standard SOP:

Each product term in an SOP expression that does not contain all the

variables in the domain can be expanded to standard SOP to include all

variables in the domain and their complements. As stated in the following steps, a nonstandard SOP expression is converted into standard form using Boolean algebra rule 6 (A + A̅ = 1)

Step 1. Multiply each nonstandard product term by a term made up of the sum of a missing variable and its complement. This results in two product terms. As you know, you can multiply anything by 1 without changing its value.

Step 2. Repeat Step 1 until all resulting product terms contain all variables in the domain in either complemented or uncomplemented form. In converting a product term to standard form, the number of product terms is doubled for each missing variable.

Example

Convert the following Boolean expression into standard SOP form:

AB̅C + A̅B̅ + ABC̅D

Solution

The domain of this SOP expression A, B, C, D. Take one term at a time.

The first term, AB̅C, is missing variable D or D̅, so multiply the first term by

(D + D̅) as follows:

AB̅C = AB̅C(D + D̅) = AB̅CD + AB̅CD̅

In this case, two standard product terms are the result.

The second term, A̅B̅, is missing variables C or C̅ and D or D̅, so first

multiply the second term by C + C̅ as follows:

AB = A̅B̅(C + C̅) = A̅B̅C + A̅B̅C̅

The two resulting terms are missing variable D or D̅, so multiply both terms by (D + D̅) as follows:

A̅B̅C(D + D̅) + A̅B̅C̅(D + D̅)

= A̅B̅CD + A̅B̅CD̅ + A̅B̅C̅D + A̅B̅C̅D̅

In this case, four standard product terms are the result.

The third term, ABC̅D, is already in standard form. The complete standard SOP form of the original expression is as follows:

AB̅C + A̅B̅ + ABC̅D = AB̅CD + AB̅CD̅ + A̅ B̅CD + A̅B̅CD̅ + A̅B̅C̅D +

A̅B̅C̅D̅ + ABC̅D

The Product-of-Sums (POS) Form

A sum term was defined before as a term consisting of the sum

(Boolean addition) of literals (variables or their complements). When two or more sum terms are multiplied, the resulting expression is a product-of-sums (POS). Some examples are

(A̅ + B)(A + B̅ + C)

(A + B̅ + C̅)( C + D̅ + E)(B + C + D)

(A + B̅)(A + B̅ + C)(A + C)

A POS expression can contain a single-variable term, as in

A(A + B + C)(B + C + D).

In a POS expression, a single overbar cannot extend over more than one variable; however, more than one variable in a term can have an overbar.

 For example, a POS expression can have the term A̅ + B̅ + C̅ but not   A + B + C. Implementation of a POS Expression simply requires ANDing the outputs of two or more OR gates. A sum term is produced by an OR operation and the product of two or more sum terms is produced by an AND operation.

shows for the expression (A + B)(B + C + D)(A + C). The output X of the AND gate equals the POS expression.

The Standard POS Form

So far, you have seen POS expressions in which some of the sum terms do not contain all of the variables in the domain of the expression. For example, the expression (A + B̅ + C) (A + B + D̅) (A + B̅ + C̅ + D) has a domain made up of the variables A, B, C, and D. Notice that the

complete set of variables in the domain is not represented in e first two terms of the expression; that is, D or D̅ is missing from the first term and C or C̅ is missing from the second term.

A standard POS expression is one in which all the variables in the domain

appear in each sum term in the expression. For example, (A̅ + B̅ + C + D)(A + B̅ + C + D)(A + B + C + D) is a standard POS expression. Any nonstandard POS expression (referred to simply as POS) can be converted to the standard form using Boolean algebra.

Converting a Sum Term to Standard POS

Each sum term in a POS expression that does not contain all the variables in the domain can be expanded to standard form to include all variables in the domain and their complements. As stated in the following steps, a nonstandard POS expression is converted into standard form using Boolean algebra rule 8 (A.A = 0)

Step 1. Add to each nonstandard product term a term made up of the product of the missing variable and its complement. This results in two sum terms. As you know, you can add 0 to anything without changing its value.

Step 2. Apply rule 12 from: A + BC = (A + B)(A + C)

Step 3. Repeat Step 1 until all resulting sum terms contain all variables in the domain in either complemented or noncomplemented form.

Example

Convert the following Boolean expression into standard POS form:

(A̅ + B + C)(B̅ + C + D̅)(A + B̅ + C̅ + D)

Solution

The domain of this POS expression is A, B, C, D. Take one term at time.

The first term, A̅ + B + C, is missing variable D or D̅, so add DD̅ and apply rule 12 as follows:

A̅ + B + C = A̅ + B + C + DD̅ = (A̅ + B + C + D)(A̅ + B + C + D̅)

The second term, B̅ + C + D̅, is missing variable A or A̅, so add AA̅ and

apply rule 12 as follows:

B̅ + C + D̅ = B̅ + C + D̅ + AA̅ = (A + B̅ + C + D̅)(A̅ + B̅ + C + D̅)

The third term, A + B + C̅ + D̅, is already in standard form. The standard POS form of the original expression is as follows:

(A̅ + B + C)(B̅ + C + D̅)(A + B̅ + C̅ + D) = (A̅ + B + C + D)(A̅ + B + C + D̅) (A̅ + B + C + D̅)(A̅ + B̅ + C + D̅) (A + B + C̅ + D̅)

Converting POS Expressions to Truth Table Format

Reca11 that a POS expression is equal to 0 only if at least one of the sum terms is equal to 0. To construct a truth table from a POS expression, list all the possible combinations of binary values of the variables just as was done for the SOP expression. Next, convert the POS expression to standard form if it is not already. Finally, place a 0 in the output column (X) for each binary value that makes the expression a 0 and place a 1 for all the remaining binary values. This procedure is illustrated in Example below:

Example

Determine the truth table for the following standard POS expression:

(A +B +C)(A +B̅ +C)(A +B̅ + C̅)(A̅ +B +C̅)(A̅ + B̅ +C)

Solution

There are three variables in the domain and the eight possible binary

values are listed in the left three columns of. The binary values that make the sum terms in the expression equal to 0 are A+ B + C: 000; A + B̅ + C: 010: A + B̅ + C̅: 011; A̅ + B + C̅: 10l; and A̅ + B̅ + C: 110. For each of these binary values, place a 0 in the output column as shown in the table. For each of the remaining binary combinations, place a 1 in the output column.

                                                                                               

                                                                                              Written by TEH WEI HAN